| Ce tutorial explique les BASES de la perspective en dessin traditionnel Nous allons rappeler quelques notions de géométrie
descriptive. Puis nous verrons différentes méthodes de division
de surfaces, |
|
| 1. NOTIONS | |
| PLAN | Surface plane, horizontale, verticale ou oblique
qui définit la zone de travail. Un plan peut être réel quand il correspond à une surface solide ou liquide, tel que dessus de table, mur, toit, plan d’eau… Un plan peut être fictif quand il est imaginé à un certain niveau ou dans une certaine orientation et que l’on peut le supposer prolongé dans tous les sens d’une façon illimitée. Il devient ligne droite lorsqu’il se présente de profil. |
| DROITE | Distance la plus courte d’un point à un autre. L’intersection de deux plans donne une ligne droite. |
| POINT | Intersection de deux droites. Lieu sans étendue, infiniment petit. Une droite qui coupe un plan donne sur celui-ci un point. Une droite qui est vue exactement par son extrémité apparaît suivant un point. N’importe quel rayon visuel partant de l’œil d’un spectateur peut être représenté par celui-ci par un point. |
| PARALLÈLES | Sont parallèles deux droites ou plusieurs qui, deux à deux, sont dans le même plan et ne se recoupent jamais, même si on les prolonge à l’infini. Peuvent être parallèles des lignes droites, des courbes ou des surfaces. |
| PERSPECTIVE CAVALIÈRE | En dessin industriel, on emploie la perspective cavalière qui donne une représentation conventionnelle des objets. Il est évident que cette perspective ne donne pas une idée exacte des objets. Cette perspective est employée dans les illustrations en pixelart avec des arêtes fuyantes à 45°. |
| PERSPECTIVE RÉELLE | Les principes de la perspective cavalière ne sont plus appliqués. Les arêtes parallèles fuyantes doivent se rejoindre en un même point, lorsque le côté d’un angle droit est fuyant dans une direction, l’autre côté fuit en direction inverse. L’aspect d’un angle droit vu en perspective varie en fonction de la hauteur de l’horizon et de l’angle par rapport au spectateur. |
| LIGNE D’HORIZON | C'est le plan horizontal principal. Il est le plan
qui se situe toujours à la hauteur des yeux du spectateur. Vu de profil,
il est le seul plan horizontal qui lui apparaisse suivant une ligne droite : la
ligne d’horizon. Quand la direction du regard du spectateur est bien horizontale, la ligne d’horizon correspond à l’axe horizontal de le vision. Quand le spectateur monte ou descend, tout le « tableau » monte ou descend également. La forme apparente des objets se modifie en fonction de la hauteur de la vue, donc de la ligne d’horizon. La place de l’horizon donne, inversement, la hauteur des yeux du spectateur, elle commande la direction de toutes les horizontales, d’où son importance. |
| CERCLE | Quelle que soit la position d’un cercle entier vu en perspective, il ne forme jamais d’angle, même quand il se raccorde à une droite. Sa courbe n’est pas un ovale, mais une ellipse. Aucune portion de la courbe ne peut se tracer au compas. |
| POINT DE FUITE | Point où des parallèles
semblent se rejoindre. Il est situé à l’infini… ou au bord de votre feuille. |
| FUYANTE | Ligne tracée vers un point de fuite ou vers un point rejoignant plusieurs autres tracés. |
| 2. PASSONS AU TUTORIAL | |
L’un des problèmes
les plus courants en perspective
est la division en parties égale d’une surface.
Carrelage, maison, mur, fenêtres, le principe de cette division
est identique pour tous ces éléments.
Imaginons qu’il soit nécessaire de diviser un rectangle en trois parties égales.
Deux méthodes sont applicables pour ce genre de
division :
le Report de Diagonales
ou le calcul sur Ligne de Mesures.
Traçons un Horizon et un Point de
Fuite
(que je nommerais P.F. plus loin).

C'est une méthode simple qui consiste à
tracer des diagonales et des verticales.
Traçons une verticale AB.
Les 2 fuyantes tracées vers le Point de Fuite nous donnent la droite verticale
CD tracée au hasard.
Nous avons un rectangle (ABCD) à diviser en trois parties égales.
Divisons la droite AB en deux, donnant le point E.
Ajoutons une fuyante de E vers le Point de Fuite.
Traçons une diagonale de B vers la droite AC, pour couper la fuyante
E ; elle donne le point F, qui redescend verticalement sur G.
Une autre verticale tracée à l’intersection de la diagonale
BF donne la droite HI.
Voilà, le principe est établi. Diagonale, verticale, diagonale, verticale et ainsi de suite en zigzag…
Une autre diagonale de H vers la droite AC coupe la verticale
FG et donne le point K, qui redescend sur J.
Nous avons coupé ce rectangle en trois parties égale en perspective
: (ABIH), (IHFG), (FGJK).
Cette technique permet de diviser des surfaces en espaces sans fin, mais il reste
une surface grisée dans le rectangle initialement tracé.
Notre calcul n’est pas bon ? Si. Oublions le rectangle original défini,
nous avons bien un rectangle (ABJK) correctement divisé en trois parties
égales, en perspective.
Alors pourquoi cette zone grisée ?
Pour diviser une surface bien déterminée, il faut appliquer une
autre méthode, plus mathématique.
Il convient d’ajouter une droite horizontale nommée Ligne de Mesures.

Reprenons notre dessin d'origine avec
un Horizon, un Point de Fuite et deux droites verticales.
Voici l’espace à partager, il s’agit de diviser
la distance AB en 5 parties égales, en perspective.
Traçons cette Ligne de Mesure, en bas, créant le point C.

Repérons deux points essentiels :
le Point de Fuite et le Point de Mesures,
tous deux sur la ligne d’Horizon.

Du Point de Mesures, traçons une
diagonale qui passe par le point E, en bas de la verticale éloignée
et qui arrive au point D sur cette Ligne de Mesures.
Divisons cette distance DC en 5 parties égales.

Une série d’obliques joignant ces 4 divisions vers le Point de Mesures
nous donnent les points FGHI qui permettent de remonter des verticales.
Notre espace est divisé en 5 parties égales, en perspective.

Cette série d’opérations donne le même
résultat en plaçant notre Ligne de Mesures
- en haut près du sommet J ou
- sur les sommets plus éloignés K et L.
Souvenez-vous en, car il est parfois
plus commode de placer la Ligne de Mesures sur l’un de ces sommets compte
tenu de l’espace disponible autour du dessin (taille de la feuille…).
Ce processus peut être utilisé indifféremment sur une fuyante
à droite.

Divisons maintenant un espace déterminé en dimensions qui se répètent
périodiquement.
Prenons une façade d’immeuble, la 2e méthode
s’applique et permet de diviser les 5 périodes régulièrement,
ce qui donne les divisions FGHI.
Ici, le Point de Mesures est situé sur l’horizon, la Ligne de Mesures
est située au-dessus pour faciliter les opérations suivantes.

Commençons par situer la porte et 2 fenêtres
sur la période A.
Traçons les fuyantes normales de la porte et des fenêtres en JK.
Les verticales nous donnent les points LMNOPQ.

A partir du Point de Mesures, traçons les diagonales
vers le haut.
Reportez ces mesures de porte LM, MN, fenêtre NO, OP, et fenêtre PQ
sur les 4 autres périodes à gauche sur la Ligne de Mesures.

Traçons toutes les autres diagonales en RSTUVW, etc.
Puis toutes les verticales qui nous donnent les tracés des 4 autres portes
et 8 fenêtres.

Appliquons cette méthode pour diviser l’angle de cette maison.
Nous allons travailler avec 2 Points de Fuite et une Ligne de Mesures.
Traçons les diagonales en partant d'un Point de Mesures central de chaque côté de l’arête de l'angle de la maison.
Le côté gauche a été dessiné plus court que
le côté droit ce qui fait que lles divisions sont différentes.
Vous pouvez imaginer qu'une fuyante du P.F. gauche vers la base de la dernière
verticale droite donnera le « rectangle » imaginaire formé
par l'arrière de la maison.

Traçons notre surface au hasard sur la feuille, en respectant l’horizon.

Une astuce en passant :
voici comment déterminer le Centre Perspectif d'un rectangle en traçant
les 2 diagonales, puis en prolongeant cette intersection centrale vers les Points
de Fuite.
Vous pouvez remarquer que les surfaces paraissent assez déformées.
Mais ce n’est pas cette surface que nous allons garder.

Cette méthode s’applique au dessin de carrelages, damiers…
Supposons cet espace carré AB, à diviser en 4 carreaux égaux.

Prolongeons la droite B vers la Ligne de Mesures en D, et divisons en 4 parties la distance CD.
Traçons les fuyantes correspondantes vers le P.F gauche.

Etablissons maintenant un nouvel élément :
le Point de Fuite des Diagonales.
C’est facile, il suffit de joindre le point C au point H, soit l’angle opposé de notre surface en prolongeant jusqu’à l’horizon.
En traçant cette diagonale, nous avons croisé les fuyantes
et créé les points EFG aux intersections.
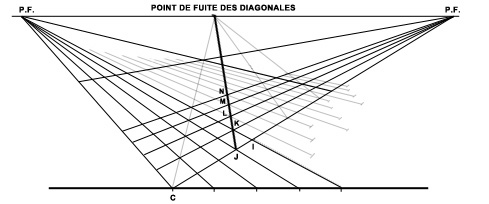
Recommençons !
Traçons cette oblique toutes les trois obliques en J, nous construisons un certain nombre de carreaux en KLMN.
La fuyante prolongée de N redonne un autre Point de Fuite de Diagonales...
et ainsi de suite.
Simple, non ?

Pas si simple que cela !
Pourquoi rester sur 2 Points de Fuite ?
Travaillons
avec le troisième Point de Fuite
ou Point de Fuite Aérien.
Toute perspective pourrait avoir 3, voire 4 points de
fuite. Nous avons jusque là travaillé sur l’espace horizontal,
voyons ce que donne l’espace vertical.
La même manipulation avec la Ligne de Mesures s’applique.
Imaginons un carré identique à la figure ci-dessus et prolongeons-le vers le bas en un parallélépipède rectangle.
Reprenons l'ordre de nos manipulations précédentes, à savoir divisons notre Ligne de Mesures, traçons les diagonales correspondantes vers le Point de Mesures. Le Point de Fuite Aérien peut fort bien ne pas être disposé verticalement sous le Point de Mesures.
On peut imaginer que notre Point de Fuite Aérien est le centre de la Terre !
représentant, par exemple, la coupe d’un immeuble avec les sous-sols et les étages,
mais cela déforme considérablement l'objet en plongée et contre-plongée.
Voir :
debullesenbulles.free.fr/Dossiers/la_perspective/plongee.html
debullesenbulles.free.fr/Dossiers/la_perspective/contre_plongee.html
Voire plus, avec 5 et 6 Points de Fuite comme sur ce lien : www.termespheres.com/perspective.html
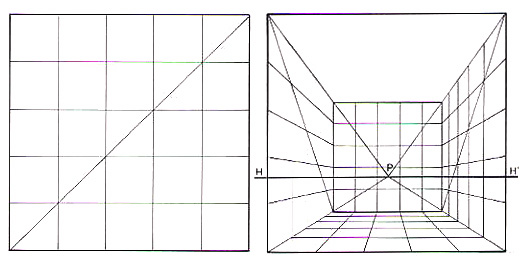
Prenons un carré, divisons le en 5 parties égales
en traçant les verticales puis les horizontales grâce à l’intersection
de la diagonale avec ces verticales.
Créons la Ligne d’horizon au niveau des yeux du spectateur en HH’,
à environ 1,80 m du sol, assez loin de chaque côtés du carré
et un Point de Fuite Central en P. Prolongeons toutes ces diagonales d'angles.
Prolongeons les horizontales du mur du fond sur les 2 côtés
vers le Point de Fuite.
L’intersection d’une diagonale tracée sur les murs de côté
permet de tracer les verticales et horizontales du mur de droite, puis les horizontales
du sol.
contenus dans cet espace, chaises, tables, cadres,
chaque « carré » donnant une échelle de taille.
Il est indispensable de travailler
sur une bonne table à dessin,
avec 2 règles dont une fixe et 2 équerres.
Pour recréer ceci sur un logiciel, Illustrator,
Freehand ou Photoshop, il est préférable de travailler dans la Palette
des Tracés et d'accumuler les tracés et les repères.
La version de Photoshop CS2 vient d'intégrer un nouvel outil très
performant de tracé et de prolongations de perspectives.

Compliquons un peu :
le mur du fond n'est pas parallèle au premier plan.
Il faut le faire pivoter sur un axe central (en pointillé).
Même manipulation pour la perspective d’angle en déplaçant
le Point de Fuite sur le côté en F, sans oublier que la droite
HH’ est toujours horizontale !
La prolongation du carré grisé nous donne le « rectangle »
AA’ et BB’.
L’angle du mur du fond est tracé.

Etablir le carré de base en perspective dite « de sentiment », c'est-à-dire comme vous le sentez au niveau de l'angle, de la profondeur et de la distance des 2 P.F. en suivant la 2e méthode.
Elever les verticales sur chaque mur et porter la hauteur « de sentiment
» en tenant compte de la hauteur de l'horizon.
Les 2 P.F. peuvent être plus ou moins espacés
: s'ils sont très éloignés l'un de l'autre, cela suppose
le spectateur à une grande distance du sujet ; s'ils sont rapprochés,
cela suppose le spectateur près du sujet.
Dans ce dernier cas, on doit veiller à ne pas obtenir des déformations
excessives qui faussent les proportions.
Soyez économes en tracés si vous voulez vous y retrouver.
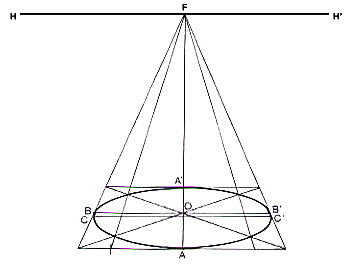
Sans entrer dans les explications de la construction d'un cercle, il est utile
d'en donner ici un dessin exact.
Si un cercle vu en perspective prend la forme d'une ellipse, il est évident
que le diamètre horizontal réel du cercle BB' ne correspond pas
au grand axe de l'ellipse : une corde du cercle CC' plus proche du spectateur
apparaît plus grande.
Le diamètre AO paraît toujours plus grand que l'autre moitié
OA' du fait de l'éloignement de celle-ci.
Les deux axes de l'ellipse restent toujours des perpendiculaires géométriques.
Il est important de bien comprendre la construction
du tracé de l'ellipse.
Il vous servira dans le dessin d'une tour de château fort, de roues de charrettes,
de roues de voitures, de tonneaux, d'arcades, d'escaliers en colimaçon,
de ressorts et de toutes sortes d'objets de formes coniques.
Quelle que soit la position d’un cercle entier vu en
perspective, il ne forme jamais d’angle, même quand il se raccorde
à une droite.
Sa courbe n’est pas un ovale, mais une ellipse.
Aucune portion de la courbe ne peut se tracer au compas.

Le problème ne se pose pas tant que le cercle est visible entièrement, c'est-à-dire qu'il se trouve dans le champ visuel.
Comment un personnage
voit-il ces 3 cercles ?

Il est ellipse quand il est entièrement visible.
Il devient parabole quand il est tangent au plan neutre, c'est-à-dire qu'il passe par les pieds du spectateur.
Il devient hyperbole quand il passe derrière celui-ci.

La
ligne d'horizon HH' doit être bien placée.
Toutes les fuyantes rejoignent l'intersection de l'horizon et de l'axe vertical.
La courbe est de plus en plus prononcée plus on s'éloigne de l'horizon.
Seule une construction très rigoureuse et précise vous permettra
d'arriver à quelque chose d'exact.

Les
cercles concentriques subissent des déformations qui correspondent les
unes par rapport aux autres. En se basant sur le déplacement de l'axe central
vu précédemment, les diamètres de ces cercles se confondent,
mais les axes des ellipses sont évidemment différents.
Aux grands axes des cercles concentriques, vus en perspective, correspond les
grandes largeurs des couronnes qui sont égales ; aux petits axes correspondent
les petites largeurs des couronnes qui sont inégales, la plus proche étant
toujours plus large que la plus éloignée.
Trois axes horizontaux différents pour ces 3 cercles concentriques.
Un seul axe vertical.
La « grande largeur » de gauche est identique à celle de droite.
Les « petites largeurs » sont toutes différentes.
Sans la perspective, notre regard sur la
vie n’aurait pas de relief.
Structure fondamentale et indispensable de l’image restituée à
nos yeux, nous ne pouvons l’ignorer.
Dessinateurs, graphistes, peintres, architectes, urbanistes le savent bien et s’attellent, tôt ou tard, à cette technique indispensable, mais de réputation ardue et « savante ».
Les premiers dessins en perspective se font vers l’âge de 6-8 ans
avec l’éternelle maison familiale dont le toit semble parfois bien
biscornu.
C’est à ce moment que l’on prend conscience de la profondeur
des objets.
JANV. 2004